『世界一わかりやすい相対性理論』シリーズの詳細版です。
アイザック・ニュートン(1642~1727)の「万有引力の法則」により、
重力の多くは解明できましたが、同時に多くの例外も発見されました。

※ 画像は「アイザック・ニュートン」;wikipedia Isaac Newtonより引用
スポンサーリンク
高校までの物理では「重力=万有引力」という誤った考え方が広まりやすい書き方が目立ちますが、「万有引力」により重力のすべてが解明されたわけでは決してありません。
ただし、万有引力の法則が間違っているというわけでもありません。
「万有引力の法則」の方が便利な事象もありますし、そもそも「一般相対性理論」では万有引力の法則を取り込んでいます。
結局のところ、相互に補い合うことで ”ある程度” 不思議な物理現象について説明がつくようになってきたという状況です。
重力の影響が小さい場所では「万有引力の法則」で十分ですし、
巨大な天体やブラックホールなどの重力の大きい場所では、万有引力の力を借りた「一般相対性理論」が必要です。
観測された現象に無理やり理屈付けするのが物理学なので、完璧な法則なんて存在しないでしょうね。
前置きが長くなりましたが、今回は『万有引力のほころびー例外はある?実例は?水星の近日点移動で詳細解説!』 として、
具体的にどういった現象が万有引力では説明できないのか(例外)を紹介したいと思います。
万有引力では説明できなくて、相対性理論では説明のつく例を挙げて、できるだけ簡潔に説明していきます。
スポンサーリンク
万有引力のほころび/|例外/実例/水星の近日点移動
万有引力の例外(水星の近日点移動)と実例
まずは「万有引力の例外と実例」から。
万有引力の法則が当てはまらない例はいくつもありますが、
最もわかりやすい「水星の近日点移動」をご紹介します。
まず大前提として、万有引力の法則が正しいならば、星の動きはすべて予測できるはずです。
主要な(質量の大きい)天体の質量をすべて調べあげ、万有引力を調べていけば、
1つの天体に加わっている ”力” は求められます。
加わっている ” 力” とこれまでどういう動きをしてきたかがわかれば、今後どういう動きをするのか予測できます。
この説明がわかりづらい場合は、車の運転を考えてみてください。

車が走っているとして、アクセルを踏めばスピードはあがります。
どのくらいアクセルを踏めば、どのくらい加速して何km/h になるのかだいたい想像できますよね。
この「アクセルを踏む」という ”力” が、万有引力の法則を使って100%求められるのです。
加えて宇宙空間では、道路の凹凸などの障害物の影響はある程度無視できます(大きい天体の場合)。
さらに摩擦力も一切働かないため、
万有引力で計算した通りに天体は動くはずなのです、万有引力の法則が100%正しいのならば…。
ところが、水星の場合のように、万有引力で計算した場所と観測した場所が全然違う例が発見されました。
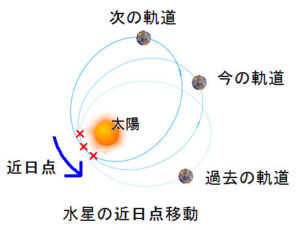
それが「水星の近日点移動」です。
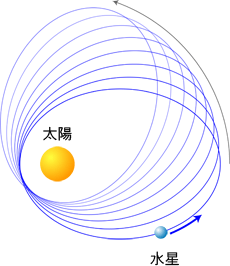
「近日点」というのは、水星と太陽の距離が最も近づく点(場所)のことです。
「近日点移動」というと、その近日点が1周ごとにずれていく現象のことを表します。
つまり、水星と太陽が一番近づく場所を毎回予測した結果を比べたということです。
計算は省略するとして、この「近日点移動」を万有引力の法則から算出すると、
100年間で531/3600度(=531秒角)ずつずれていく計算になります。
※ 「秒角」というのは角度の単位で、1秒角は1/3600度に相当します
しかし、実際に水星の近日点移動を観測すると、100年間で574秒角ずつずれていくとわかりました。
誤差は100年間で43秒角と小さいように感じられますが、確実に万有引力による結果とは違う結果となりました。
つまり、水星の近日点移動は完全なる万有引力の例外だったのです。
スポンサーリンク
万有引力の例外:「アインシュタインによる新提案」
人間というのは過ちを認めたがらない生き物で、
新たな発見があっても「何かの間違いだ」と決めつけてしまう傾向にあります。
水星の近日点移動の時も、水星の内側にもう1つ惑星があるんじゃないかというバルカン説や、
太陽が球体じゃないから計算式が間違っているなどさまざまな説(言い訳)が考えられました。
ここに鋭くメスを入れてきたのが、20世紀最高の科学者ともいわれるアルバート・アインシュタインです。

アインシュタインは自身の相対性理論の中で、空間は絶対的な存在ではないと提唱しました。
つまり、水星の近日点移動が万有引力と合致しないのは、
太陽の質量によって周りの空間がゆがんだ結果だと説明したのです。
これは、重力によって宇宙空間はでこぼこしていて、斜面に沿って天体は運動しているということです。
ルーレットで球が回り続けているように、地球も太陽の周りを回り続けていると考えたのです。
ルーレットの場合、摩擦によって次第に球は減速して落ちていきますが、
宇宙空間には摩擦力が存在しないので、いつまでも回転できるのです。
車の例を再び取り上げれば、
「車が動いているのは、坂道を下っているからであって、アクセルを踏んでいるからではない」という考えに相当します。
にわかには信じられないかもしれませんが、
現在では「重力は空間を曲げる」という一般相対性理論の考えは広く支持されています。
「重力は空間(光)を曲げる」という記事で詳しく解説しているので、興味のある方はそちらも読んでいただけるとありがたいです。
他にもアインシュタインは、空間だけでなく ”時間” も絶対性のある存在ではない、つまり「相対性」の存在だと述べました。
空間も時間も、観測する人間によって異なる…常識的には理解しがたいかもしれませんね。
アインシュタインが「特殊相対性理論」を発表したのは彼がわずか26歳のときです。
ちなみに「E=mc2」という式も同年に提示され、「一般相対性理論」は36歳の時です。
さすがとしか言いようがないですよね。
あまりアインシュタインについて語っていても読みづらくなるだけなので、今回はこの辺で終わりにしましょう。
以上、『『万有引力のほころび』 ー例外はある?実例は?水星の近日点移動で詳細解説!』でした!
最後までお読みいただき、ありがとうございました<(_ _)>
「万有引力の例外(水星の近日点移動)と実例」まとめ
万有引力の例外(水星の近日点移動)と実例
・ 万有引力の法則により、重力の多くは解明できた
・ しかし、水星の近日点移動は、万有引力で計算した場所と観測した場所が大きく異なっていた
・ 万有引力だけでは説明のつかない現象があることがわかった
・ 現在では、一般相対性理論による「重力が空間を曲げている」という考えが広く支持されている
・ ただし、万有引力の法則が誤っているわけでは決してなく、一般相対性理論では万有引力の法則を活用している