「ゼノンのパラドックス」という言葉を聞いたことがありますか?
「ゼノンのパラドックス」とは、「目的地には永遠にたどり着けない」という矛盾(パラドックス)の考え方です。
今回は『ゼノンのパラドックスーウサギは亀には永遠に追いつけない?』として、ちょっと興味深い矛盾もどきに解説します。
盲点を突かれるような興味深い内容である一方で、まったく難しい話ではないので、明日の話のタネ用にぜひお読みください。

スポンサーリンク
ゼノンのパラドックス/ウサギは亀には永遠に追いつけない?
ゼノンのパラドックス「目的地にはたどり着けない?」
ゼノンのパラドックスで最も面白い点は「目的地にはたどり着けない」ような感覚に陥ることです。
ある目的地に到達するためには、まずその目的地の半分の地点を通過しなければなりませんね。
さらに、その中間地点を通過してから目的地を目指すには、そこと目的地との半分の地点を通過する必要があります。
さらにその中間地点と目的地との半分の地点、また半分の地点…、また……。
こうすると限りなくゴールには近づくのですが、無限に中間地点ができて、
永遠にゴール地点にはたどり着けないことになります。
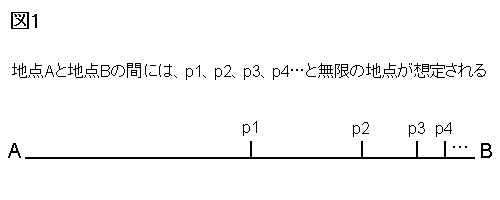
つまり、私たちが目的地に到着することは不可能です。
これが「ゼノンのパラドックス」そのものです。
この「ゼノンのパラドックス」の考え方のどこがおかしいと思いますか?
「目的地に着けない」という結論は、明らかに私たちの現実と矛盾します。
1m先まで行こうと思えば一歩で行けるのに、永遠につけないということは考えられません。
しかし、目的地の中間地点が永遠に増える以上、確かにいくらやっても目的地への到達は不可能です…。
スポンサーリンク
ゼノンのパラドックス「カギは時間」
では、ゼノンのパラドックスの答えです。
これは「時間」という概念を無視していることから生じる「みかけ上の矛盾」です。
例えば、目的地まで1秒で到達すると考えましょう。
その場合、中間地点までは何秒かかりますか?
そうです、0.5秒(=1/2秒)ですね。
そこから目的地を目指す場合、次の中間地点までは何秒かかりますか?
0.25秒(=1/4秒)ですね。
このようにして、「目的地までにある無数の中間地点」に到達するまでの時間をすべて足していってみましょう。
最初は1/2秒、次が1/4秒、その次が1/8秒……。
すべて足すと、
(1/2)+(1/4)+(1/8)+(1/16)+(1/32)+(1/64)+……(1/2n)+………。
この答えは限りなく「1秒」に近づきます(収束)。
つまり、「中間地点を無限に通過しなければいけないから永遠にゴールできない」というのは「1秒以内での出来事」だったわけです。
そのため、1秒後にはきちんと目的地に到達できるわけです。
今回の「ゼノンのパラドックス」は哲学者のゼノンが提唱したのですが、
彼は「時間」という概念を忘れていたことに加えて、
「無限に続く数字をすべて足したら、答えも無限になる」という勘違いをしていたために頭が混乱してしまったようです。
「無限に続く数字を足したら、答えも無限」というのは、意外と忘れがちな事実かもしれません。
忘れてしまったときは、今回取り上げたような、
(1/2)+(1/4)+(1/8)+(1/16)+(1/32)+(1/64)+……(1/2n)+………
という無限に続く足し算を思い出してください。
この足し算は、決して1を超えることはありません。
なぜなら、後半にいくにつれて値がどんどんゼロに近づいていくからです。
もっとわかりやすく言えば、小数点の 0.000000000000……という長さを更新していっているだけで、
上の位を押し上げることは決してありません。
以上のように、少し見方を変えるだけで真実が見えてくるというのは、数学の醍醐味の1つでもあります。
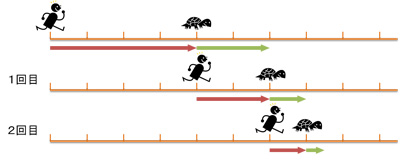
ちなみに、「アキレスと亀のパラドックス」というアキレスさんが永遠に亀に追いつけないという「みかけ上の矛盾」も
今回の「ゼノンのパラドックス」です。
以上、『ゼノンのパラドックスーウサギは亀には永遠に追いつけない?』でした!
最後までお読みいただき、ありがとうございました<(_ _)>
「ゼノンのパラドックスーウサギは亀には永遠に追いつけない?」まとめ
ゼノンのパラドックス
・ ゼノンのパラドックスとは、目的地までの中間地点が永遠に更新されるため、限りなく目的地に近づくがそこにはたどり着けないとする矛盾
・ 矛盾の原因は「時間」の概念を忘れていることに起因する
・ 目的地までの所要時間を t 秒とすると、t 秒以内での距離を分割して考えているに過ぎない
・ よって、 t 秒後には確かに目的地に到達する